α-SiO2 是石英物质和硅酸盐的重要组成部分，而且是地球上储量最丰富的物质。石英晶体在常压下 有多种晶体结构：如 α-SiO2，β-SiO2，α-磷 SiO2，β-磷SiO2以及α-方SiO2，β-方SiO2等等。其中石英α-SiO2 是常温常压下最稳定的晶体。

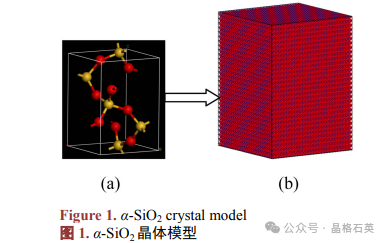
在二氧化硅中，硅位于正四面体的中心，4个氧原子位于正四面体的4个顶角上，图1(a)表示二氧化硅在体心立方结构中的晶胞。然后根据笛卡尔坐标构建立了 α-SiO2的 晶体结构(如图 1(b)所示)。其中，晶格常数a=4.978 埃，b=4.978 埃，c=6.948埃，盒子的长度为30a×30b×30c，总的原子数为324,000个，在xyz三个方向上采用周期性边界条件。

在分子动力学的模拟过程中，我们采用的 tersoff 势函数描述 Si-O 之间的相互作用。然后在 NPT 系综下，时间步长1fs，应用 Nose-Hoover 热浴的方法在常温下进行弛豫，弛豫步数20,000 步。 图2为模型弛豫过程中能量变化图，从图中可以得到晶体模型在10ps后达到平衡。然后在NVT系综下 进行单轴加载，应变率为1×109s−1 ，这时仍用 Nose-Hoover 热浴的方法控制系统的温度使其保持在相应的温度条件下。然后在常温300K下模拟石英 α-SiO2 晶体的拉伸力学性能。模拟结果讨论分析中我们应用 CNA 结构分析方法来分析体系中微观结构的演变，利用 Ovito 软件观察原子结构，应用 LAMMPS 代码来模拟拉伸力学性能。

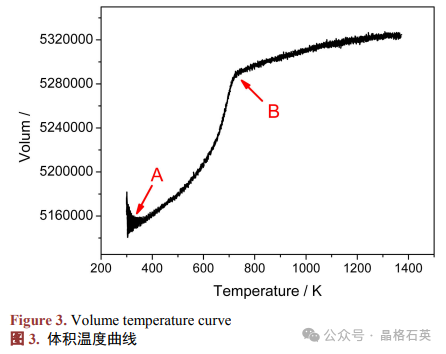
α-SiO2体积随着温度升高的变化曲线

下图为 α-SiO2 的体积温度曲线。从图中可以得到随着温度的升高晶体的体积出现了A和B两个变化拐点。在A点时，晶体从四面体结构中逐渐的析出非晶结构。随着温度的升高，体积以非线性的形式快速的膨胀，晶体的非晶化程度比重也迅速的增加。到了B点时，整个晶体结构完全非晶化，晶体结构趋于稳定，然后随着温度的升高晶体的体积缓慢稳定的增加，结构逐渐进入融化阶段。

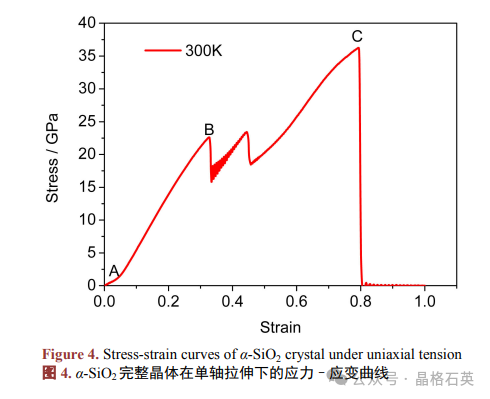
α-SiO2晶体在外载下的力学性能

下图为石英 α-SiO2 的完整晶体在常温下单轴拉伸的应力–应变曲线。应力–应变关系反映了材料的 基本力学性能，从图中可以得到随着应变的增加石英 α-SiO2 晶体在应变为 4.7%时出现了弹性极限(如图 4 中 A 点)，应力与应变表现出非线性关系。A 点后晶体进入弹性变形阶段，应力与应变呈线性关系，此 时材料结构没有发生形变。当加载的应变到达 32.6%时，晶体的内部应力达到第一个屈服点，屈服应力 22.6 GPa。随后晶体进入塑性变形阶段，然后随着外载的逐渐增加，从图中可以得到应力在 B 点和 C 点 之间出现了上下震荡，纳米晶体进入塑性变形阶段，而且开始发生非晶化相变。应力过了 C 点之后，由 于晶体结构完全非晶化，随着加载的进行，应力逐渐增加，一直达到曲线的锋值——断裂强度(36 GPa)， 晶体开始进入断裂阶段。接着随着应变的增加应力急速下降到零，此时晶体完全断裂。因此，从图中可 以看出，石英 α-SiO2 晶体在常温单轴拉伸过程中经历了弹性阶段，塑性阶段(非晶化相变)以及断裂阶段， 弹性模量达到了 69 GPa，具有很高强度。

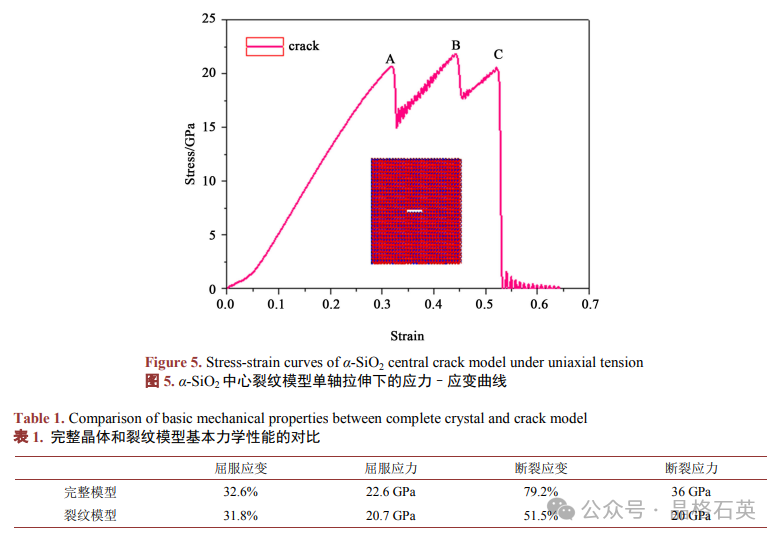
α-SiO2晶体中裂纹扩展的力学性能

下图为石英 α-SiO2 在常温下裂纹模型单轴拉伸时的应力–应变曲线。从图中可以得到随着应变的增 加石英 α-SiO2 裂纹晶体在应变为 31.8%时，应力达到最大的屈服点，屈服应力 20.7 GPa (如图中 A 点所 示)。相对于完整晶体的屈服应力和屈服应变出现了下降(如表 1 所示)。由此可以得到微裂纹可以降低石 英晶体的力学性能。然后晶体由弹性变形阶段进入塑性变形阶段，随着外载的逐渐增加应力在 A 点和 C 点之间进行上下的震荡，石英晶体结构展现出很好的塑性，能延缓微裂纹的快速扩展，同时纳米晶体结 构也开始发生非晶化相变。当加载应变过了 C 点之后，由于晶体结构完全非晶化，随着加载的进行，应 力逐渐增加，一直达到曲线的锋值——断裂强度(20 GPa)，晶体开始进入断裂阶段。这个数值远远低于完 整晶体结构。因此，微裂纹使晶体的断裂强度出现大幅度的下降，这主要是由于结构的非晶化降低了结 构的塑性，使得裂纹尖端的应力集中现象得不到有效的缓解，裂纹进入快速扩展阶段，接着随着应变的 增加应力急速下降到零，直到晶体完全断裂。

留言

写留言