在多晶硅定向凝固过程中杂质分凝的研究时，假定其条件稳定，将其看作一个细长等界面柱状的多晶硅定向凝固体系，其液固界面以平面状沿轴方向推进的凝固。在该体系中杂质的等浓度面被看成一个平面，并且其法线矢量与结晶方向一致，因此可以认为是一个一维的问题，只要对具体的条件做一些规定即可求解。多晶硅的定向凝固的过程是无法达到平衡凝固的状态，多晶硅的平衡态凝固也只有在液相和固相中杂质都能完全扩散时才能达到。

多晶硅固液界面的温度为其熔点温度，杂质在液相中的扩散系数一般在 10^-9 m^2/s数量级，而在固相中的扩散系数一般在10^-12 m^2/s数量级。可以假设固相完全无扩散而液相充分扩散(完全混合均匀)。

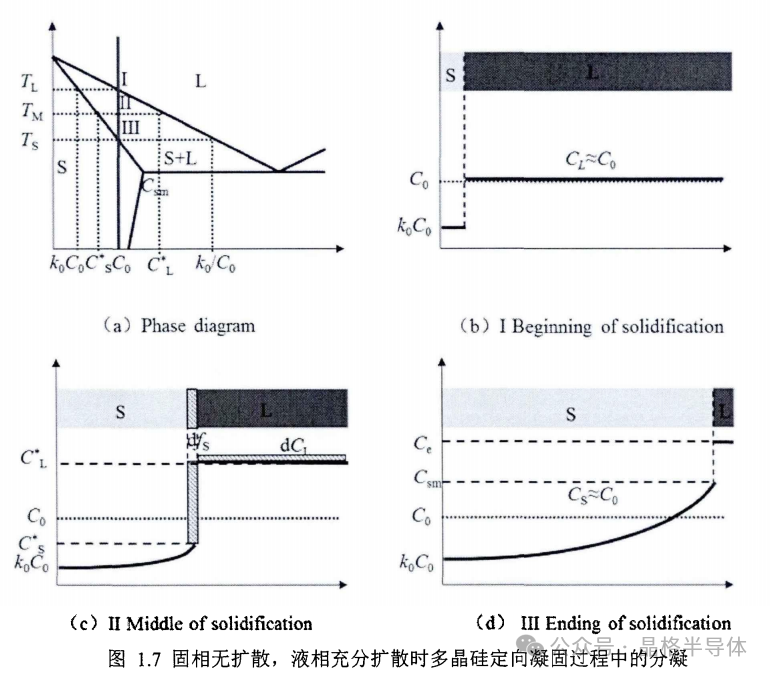
以原始杂质含量为 C0的多晶硅的定向凝固过程为例，分析该假设条件下多晶硅定向凝固过程中的杂质分凝。当定向凝固开始时，最开始形成的固相成分按照平衡相图1.7(a)所示为 k0C0。由于固相中无扩散而液相中充分扩散，已经凝固的固相杂质成分将保持不变而液相中杂质成分始终保持均匀，如图1.7(b)所示。由于 k<1，随着凝固的继续进行，硅熔体中杂质的含量升高，所以后续凝固的固相中杂质的含量也会逐渐升高。当温度为 T*时，固液界面处，含量为Cl的液相,析出的固相中杂质含量为 Cs，如图 1.7(c)所示。当凝固即将结束时，在凝固方向上结晶出的固相中溶质含量如图1.7(d)所示。

方程(1.6)和(1.7)即为著名的 Scheil方程，又称为非平衡凝固杠杆定理。根据固相和液相的体积分数，可以得到此时的固相或液相浓度及凝固过程中固相成分的变化规律，即多晶硅内偏析规律。

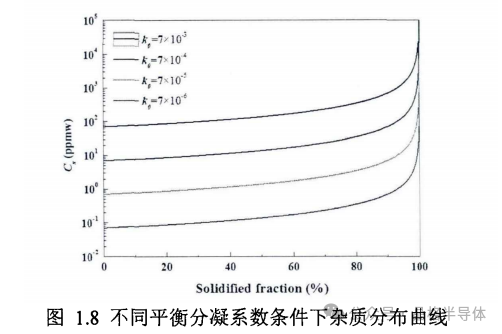
根据 Scheil 方程，不同的分凝系数k定向凝固条件下固相杂质浓度Cs随凝固部分随着凝固分数大变化的曲线如图1.8所示。利用 Scheil 方程能很好地描述出晶体生长速度不大时的溶质再分配的规律。但是值得注意的是，例如当fs等于1时，由图看到，Cs等于无穷，这显然是不可能的。在 Scheil方程的推导过程中，忽略了凝固时任何体积的变化而是假设 k0是常数，并假设任何时刻溶质，在熔体中的分布是完全均匀的。这些假设与实际情况是有差异的。因此，Scheil方程只是一个近似的表达式，不能在整个fs范围内成立。在实际的凝固系统中，由于液相中溶质浓度不断增加，尤其在凝固后期，当达到共晶成分点时，Scheil方程就不适用了。

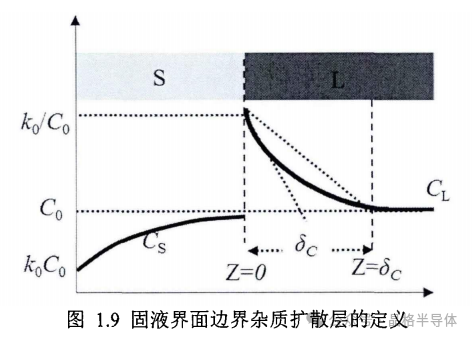
多晶硅凝固过程中，在硅熔体中只存在杂质扩散时，扩散层的厚度是最大的，凝固出的固相杂质成分和多晶硅原始杂质成分相同，达到稳态凝固。固液界面附近凝固的固相排出的溶质含量，与溶质边界层内扩散到远处液相的溶质含量相等，所以凝固界面前沿的溶质富集区保持稳定，其等效边界层(δc)长度被定义为等于 2D/v，如图1.9所示。

在实际凝固过程中，液相完全混合和只有扩散的情况都是极少遇到的，通常定向凝固都是从底部向顶部凝固，是在重力场中进行的，在硅熔体中存在自然对流。即液相中既有杂质的扩散也有对流搅拌。

将多晶硅生长的过程简化成为一维平面结晶过程，其溶质的再分配是由界面分凝和扩散过程控制的。假设条件:固液界面是平界面;忽略固相中杂质的扩散;不考虑多晶硅液固相密度的变化和溶质蒸发引起的溶质迁移;固液界面为平衡界面，杂质在固液界面处分凝系数始终保持不变

当扩散是杂质唯一传输机制时，只有熔体长度无限长时，Cl才趋近C0；而当液相中存在对流时，对流促使杂质快速混合均匀。此时在固液界面会形成杂质扩散边界层宏观流动平行于界面层流，在扩散层内部，杂质只能依靠扩散(D为扩散系数)传输。

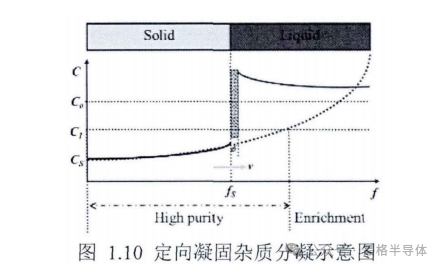
多晶硅定向凝固过程中，杂质在固相液相以及固液界面处的分布如图 1.10所示。当结晶前沿的液相中存在较为强烈的对流时，会加速液相中的溶质传输，促使界面前沿的溶质富集区的厚度减少，液相内部的溶质浓度随着结晶过程的进行而迅速增加，出现图中的溶质再分配的特性。开始凝固的多品硅杂质含量低于目标杂质含量 形成提纯区凝固末端即铸锭上部形成富集区域。